Глава 10

Сферическая аберрация.

Наиоблее рапространенное присутствующее на стекле искажение называется сферической аберрацией. Она в разной степени присутствует на любых поверхностях и необязательно должна становиться ослабляющей передачу изображения, все зависит от ее серьезности.

Звездный тест на сферическую аберрацию удивительно чувствителен и легоко для интерпретации. Эта глава описывает пять тем:

1.        Волновые фронты, деформированные простой сферической аберрацией (кривые четвертого порядка) узнаются по поведению света приближенному к каустике лучей. С одной стороны фокуса свет берется из внешних частей внефокального диска и откладывается в его центре. С другой стороны фокуса свет забирается из центрального поярчения наиболее удаленными кольцами.

2.        Сила сферической аберрации более низкого порядка может быть грубо оценена с помощью использования центральной преграды и сравнением точек разрыва центральной тени по обеим сторонам.  Чтобы эта техника оценки была правомерна, корректирующая ошибка должна быть только сопутствующей аберрацией.

3.        Сферические аберрации более высокого порядка, несмотря на то что заметны в звездных тестах определенного плана, практически никогда не видны в чистой форме.

4.        Вычисляя энергию собранную внутри углового радиуса l/D (близко к краю дифракционного диска), пользователь телескопа может с пользой собрать вместе комбинированные эффекты сферической аберрации и центральную преграду. Ткое отношение круговой энергии имеет много схожего с отношением Стреля, но включает ухудшение от преграды в одиночном стандарте.

5.        Четвертная длина волны коррекционной ошибки передает изображение протяженных объектов, становящихся заметно смягченными, но едва ли приемлема.

10.1 Что такое сферическая аберрация?

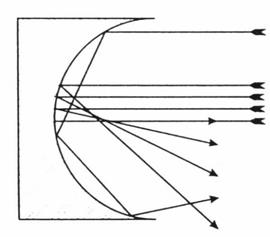
Поскольку они имеют форму неглубоких чаш или выпячиваний, естественно предположить, что совершенные зеркала и объективы это части сфер. Однако, сфера не лучшая геометрическая форма для передачи изображения. Следующий мысленный эксперимент делает эту мысль очевидной. Вообразите внутреннюю поверхность полусферы зеркалом и свет и свет попадающим в него справа от бесконечно удаленного источника как это показано на рис. 10-1. Свет, ударяющийся в края,  едва отражается; он целует внутреннюю часть сферы и рикошетирует в пределах половины купола. Свет, попадающий ближе в направлении центра, отражается по направлению к некоторому фокусу, но свет ударяющийся близко от оси направляется в дальше всего. Область фокуса расширена на рис. 10-2  для того, чтобы показать, что фокус отклоняется от геометрической точки в рожкообразную каустическую огибающую.

Рис.10-1. Полукупольное сферическое зеркало. Фокус наиболее сложно определим когда прибывающий свет приближется к краю.

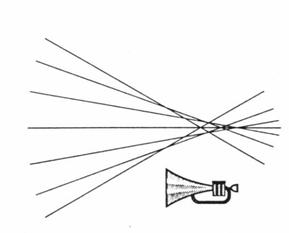
Рис. 10-2. Каустический «рожок».

Первоначальный смысл слова каустика – «сжигание», так оптическая каустика представляется вблизи фокуса. В прослеживании луча,  этот термин обретает едва другой смысл. Каустика – кривая или поверхность, вдоль которой, луч, кажется, скучивается. Он отсылается к положениям, где геометрическое распространение или схождение лучевого пучка не выдает правильной величины интенсивности. Каустики места, где нужно прибегнуть к теории дифракции.

Вид сферической аберрации представленный на рис. 10-1 называется сферическим недоисправлением. При переисправленности картина обратная. Центрально падающий луч пресекает ось слишком близко к объективу, и свет, падающий у края, пересекает ось в ниболее удаленной точке. При переисправленности рожок указывет в другую сторону.

Наилучшая конфигурация поверхности для отображения света изменяется от телескопа к телескопу. Некоторые объективы, такие как составные линзы рефрактора, исправляются за сферическую аберрацию изгибанием (?) или разделением сферических поверхностей. Здесь производитель использует этот прием для того, чтобы сохранить легко создаваемую сферическую форму. Сходное изгибание присутствует в системе Максутова. Скорлупа мениска на самом деле не имеет большой фокусирующей силы потому, что задняя поверхность имеет приблизительно ту же самую кривизну, что и передняя. Преследуемая цель – изменение аберрации. Другие телескопы разделяют обузу корректировки сферической аберрации главного фокусирующего элемента с необычно деформированной пластиной корректора, как это распространено в Шмидт-Кассегренах.

Что касается телескопов с одним  фокусирующим зеркалом (т.е. Ньютоновских рефлекторов), верная геометрическая форма – параболоид. Ровное вторичное отражает луч так, что голова наблюдателя не попадает в оптический путь, но не учавствует в формировании изображения. Параболоид особый случай в семействе поверхностей именуемых коническими сечениями вращения.

Классический Кассегрен объединяет парболическое основное зеркало с гиперболическим вторичным для достижения требуемой сферической коррекции. Можно убрать вторичное зеркало из классического Кассегрена и установить диагональ как ее используют в Ньютонах. Вторичное зеркало должно исправлять ему свойственную сферическю аберрацию независимо. Можно резонно догадаться, что вторичное зеркало должно бы быть выпуклым параболоидом, но вторичное не выполняет той же работы, что основное, так что оно должно быть изогнуто иначе[22].

Другие Кассегрено-подобные инструменты, такие как типа Долл-Киркхама, корректируют лишь часть сферической аберрации всей системы на кажном зеркале. Выпуклое вторичное остается сферическим. Это зеркальце добавляет компонет сферической аберрации противоположного знака к вогнутому сферическому основному, но этого количества недостаточно для того чтобы совершенно скорректировать систему. Как следствие, правильно сделанное основное зеркало Долла-Киркхама деформируется до вытянутого сфероида (между сферой и параболоидом). Долл-Киркхамы популярны среди изготовителей телескопов потомучто сферическое вторичное зеркало легко сделать. Однако, они страдают серьезной внеосевой комой.

Разработка Ричи-Кретьена идет по другому пути. Образуя более серьезно гиперболизированные кривые на обоих главном и вторичном зеркалах, производитель может достичь более высокой степени коррекции комы посравнению с классическим Кассегреном. Но, эти телескопы очень трудно изготовить, и обыкновенно являются пердметом интереса только больших обсерваторий. Космический телескоп Хаббла – Ричи-Кретьен.

10.2. Космический телескоп Хаббла.

Лето 1990 года ознаменовалось событием, сделавшим темой передовиц сферическую аберрацию, до этого понятную лишь для посвященных. Космический телескоп Хаббла (HST), как оказалось, был сделан неверно. Газетные сообщения гласили, что он страдает от приблизительно  ½ длины волны сферической аберрации и, что край зеркала отсутствует приблизительно на 2 микрона (или 2 mм).

Вопервых, эти утверждения были запутаны. 2 mм ошибка поверхности могла бы заставить волновой фронт неправильно искривляться на 4 mм, или 7.25 длины волны желто-зеленого света. Если фокус подстраивается ближе к минимальному размеру диска, чем к фокусу центра, эта величина уменьшается на коэффициент от 4 до 1.8 длин волн.

Это число объяснилось, когда статья в Sky&Telescope упомянула, что аберрация в ½ длины волны измерялась как среднеквадратичное (RMS) отклонение (Sinnot 1990a).  Чтобы вывести величину пик-подошва из RMS величины, мы должны умножать на коэффициент приблизительно 13.4 / 4, из-за погрешностей фигуризации

   1                                                                         1

¾¾ длины волны (пик-подошва) =  ¾¾¾¾ длины волны (RMS)

   4                                                                       13.4

(10.1)

    1                                                      13.4

отсюда      ¾¾ длины волны RMS * (¾¾¾¾¾¾) =1.68 длины волны.

    2                                                         4

Сравнение, наиболее известное любителям  - с ¼ длины волны допуском Рэлея – в этом вычислении приводит к 1.7 длинам волн для HST, предполагая, что ½ длины волны RMS ошибка была точна.

Основной причиной ошибки было неправильно собранное устройство называемое нуль-тестер примененное в производстве основного зеркала. Отсюда, зеркало неделавшее этой поправки могло бы быть совершенно точным. К сожалению, нуль тестер был размечен неправильно и дал неверную обратную поправку сферической аберрации (S&T 1990; Capers и дрю 1991).

10.3. Обобщенная сферическая аберрация.

С точки зрения звездного теста, вам не требуется размышлять о формах оптических поверхностей, или даже вспоминать их длинные названия. Рассматривайте форму окончательного волнового фронта только как вычтенную из совершенной сферы. Разность может быть расширенно изложена  в форме простой многочленной функции:

W(r) = A₀ + A₂r² + A₄r⁴ + A₆r⁶… (10.2)

где r радиальная координата, изменяющаяся от 0 до 1. Знак W(r) стоит для обозначения общей дисторсии этого  волнового фронта от сферы с центром в фокусе. Если W(r) равно нулю, тогда кривые одинаковы. Посмотрим на каждый из этих членов и коэффициентов перед ними (обозначенных буквами А) и порассуждаем, что они из себя представляют.

Первый – константа, А₀, ускоряющая или тормозящая волновой фронт. Мы можем думать об этом числе как о константе «времени» или «фазы», и оно должно выбираться так, чтобы сфера сравнения не слишком удалялась от волнового фронта. Эта константа обозначает распространение, с различными величинами А_0, представляющими моментальные снимки сделанные в разные моменты времени. Обычно, эта константа равна нулю, когда волна непосредственно проходит через апертуру или иначе подстраивается для удобства.

Член A₂r² гладкое изгибание, либо проталкивние волнового фронта немного вперед, либо некоторое его оттягивание. Если центр нашей эталонной сферы располагается в неправильной фокальной точке, этот член принимает на себя главный удар возрастания. Таким образом, A₂r² здесь называется «аберрацией дефокусировки», и представляется на рис. 4-15.

Дефокусирующий член A₂ может быть умозрительно включен в пространное разложение сферической аберрации, и с точки зрения звездного тестирования, дефокусировка должна рассматриваться лишь как еще одна аберрация. Однако, дефокусировка не является свойством самомого стекла, поэтому не в обычиях относить ее к членам сферической аберрации. Дефокусировка настолько важна, что она оставляется в стороне и рассматривается отдельно.

Член четвертого порядка, A₄r⁴, то, что обыкновенно и считается сферической аберрацией. Другое название этого члена – сферическая аберрация главного зеркала. Погрешности, описанные здесь - погрешности «фигуризации», такие как недо- или переисправленность.

Члены A₆r⁶ и далее … обычно малы, но могут стать важными в непривычных оптических системах. Нетрудно заметить, что у эллипса это протяжение ряда идет бесконечно, но каждый коэффициент A_n обыкновенно намного меньше, чем предыдущий. В этой главе, мы можем рассматривать коэффициент A₆, как последний важный член последовательности.

Сферическая аберрация может выражаться некоторым числом равно справедливых последовательностей. Другой способ обращения к членам волнового фронта четвертого и шестого порядка называть их сферической аберрацией третьего и пятого порядка. Эти наименования происходят от отклонения волнового фронта, не от самого фронта волны, и как далеко свет смещается в стороны от центра дифракционного пятна. Некоторые авторы находят это более удобным для рассмотрения вычетных изменений на фокальном расстоянии c отклоноением r, или «долготной аберрации» (Kingslake 1978, стр. 114). В этом способе рассмотрения погрешностей, аберрация главного зеркала - коэффициент члена r². Так, мы можем найти ту же самую сферическую аберрацию главного зеркала, выраженную коэффициентами четвертого, третьего или второго порядка, в зависимости от того имеет ли отношение расширение многочлена к волновому фронту, к вычитному отклонению или к долготной аберрации соответственно. В этой книге мы всегда будем касться только фронта волны.

10.4. Функции Аберрации.

Аберрации, как правило, измеряются от положения наилушего фокуса[23] потому, что кажущийся диск там минимален. Это то, что мы думаем, когда говорим: «телескоп сфокусирован». Когда A₂ равно нулю, равенство 10.2 имеет положение фокуса произвольно установленного в месте называемом «параксиальным (равноосным) фокусом», или  фокусе центра зеркала или объектива (узкий конец каустического рожка сверху). Несмотря на удобное место для вычисления формы фронта волны, оно не имеет никакого отношения к положению, где мы визуально обнаруживаем наименьший диск. Если мы сделаем константу A₄ не нулевой, например, мы обнаружим, что должна быть добавлена некоторая дефокусировка для того, чтобы догнать наилучший фокус, поскольку тот удирает. Если мы изменим A₄ во второй раз, нам придется перемещать фокус снова. Член A₆ создает еще больше сложностей. Если мы пожелаем установить чистые, самого верхнего порядка сферические аберрации в наилучшем положении фокуса, нам придется лишь вычесть правые величины низших порядков. Устранение этих членов может быть утомительным, хотя способ вычисления прост.

Гораздо более удобно, вычленить волне достаточное количество аберраций низших порядков, чтобы автоматически отбросить их от каждого возрастающего члена. Этот шаг был предпринят, в сравнительно более сложной форме, Фрицем Цернике (Fritz Zernike), и результирующие члены назваются ортогонаяльным многочленом Цернике (Борн и Вольф 1980). Интересующие члены ограничиваются здесь четвертым и шестым порядками, но для высших порядков они также существуют:

W₄(r) = 4A¢₄ (r² + r⁴ + ¹/₆)

                                                                                                       (10.3)

W₆(r) = -½A¢₆ (20r⁶ - 30r⁴ +12r²-1)

 Примы (штрихи) расставлены на коэффициенты с тем, чтобы показать, что они не те же самые величины как в ур. 10.2.

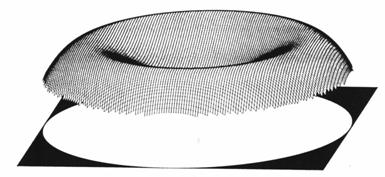
Рис. 10-3. Аберрация функции Цернике W₄(r), демонстрирующая переисправленность в наилучшем фокусе.

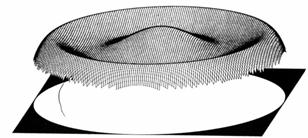
Рис. 10-4. Аберрация функции Цернике W₆(r), описывающая сферическую аберрацию более высокого порядка. 

Эти сложно-выглядящие уравнения кое-что упрощают, когда изображаются как функции аберрации (см. рис. 10-3 и 10-4). Все сфокусированные образцы представленные ниже соотносятся с около-фокальными  положениями, подразумеваемыми в этих функциях.

Вид функции многочлена Цернике четвертого порядка имеет всего лишь одно пончикообразное кольцо, тогда как более высокого порядка имеет завитый край по другую сторону. Восьмой, десятый и более высокого порядка многочлены добавляют по одному завитку каждый. Фактически, когда мы поднимаемся выше, образец выглядит возрастающе волнистым. Но запомните,  сумма всех этих многочленов передает гладкую поверхность. Знаки и амплитуды выбираются так, что вид «стиральной доски» пропадает. Только для зональных дефектов главы 11 аномальные вклады многочленов высокого порядка, суммируются, чтобы в итоге дать не нулевой резултат.

Хотя это не отражено на чертеже, функция шестого порядка имеет более закрученную каустическую форму.  Вообразите как если бы очень могучий индивидуум, влез в раструб музыкального рожка на рис. 10-2. и вытянул мундштук наполовину в обратном направлении через этот раструб. Получившийся в результате ущерб был бы очень похож на эту каустику (Канье и др. [Cagnet et al.] 1962).

Другая печальная особенность заключается в том, что положение дифракционного фокуса слегка сдвигается, если телескоп диафрагмируется. Большинство образцов показанных в этой главе берут в расчет это изменение. Исключением являются образцы продольных срезов.

10.5. Коррекционная ошибка (Сферическая аберрация более низкого порядка)

10.5.1. Фильтрация сферической аберрации.

Модуляционная передаточная функция (MTF) изображена на рис. 10-5. Сползающие линии показывают манеру понижения контраста, когда сферическая аберрация медленно усугубляется. Одна интересная черта состоит в мягком возрастании, что имеет место для слабых аберраций на пространственной частоте 0.5 - 0.6 от максимума. Это улучшение соответствует частоте, где расстояние штрихов на штрих-тесты (штрих-тесте), является расстоянием до первого дифракционного кольца. Оно сходит на нет с противоположной стороны.

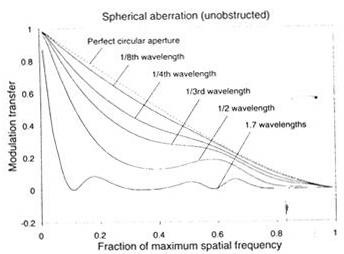
Рис. 10-5. МПФ характеристика коррекционной погрешности.

МПФ заметно ухудшается, когда зрачек апертуры идет от 1/8 до ¼ длиы волны полной аберрации, подчеркивая, что оптическое качество начинает ухудшаться в районе ¼ длины воны коррекционной погрешности.

Сферическая аберрация сдвигает свет от центра диска к внешним частям дифракционной структуры. Необычная черта сферической аберрации состоит в том, что она не касается цетнральной сердцевины изображения (до тех пор пока аберрация не станет достаточно сильной), иначе как чтобы лишить ее сока ее интенсивности. Сферическая аберрация высасывает энергию из центрального диска Эри и кормит ею кольца. Этот почерк выделяет сферическую аберрацию среди прочих (даже мягкая дефокусировка показывает это особое поведение). Энергия переносится из центрального диска искаженного зрачка, но форма довольно хорошо сохраняется неискаженной вплоть до перврго дифракционного кольца. Также, на рис. 10-6. отношение круговой энергии для ¼ длины волны сферической аберрации встречает нулевой радиус у отметки 0.8, где ему следует это делать по отношению Стреля.

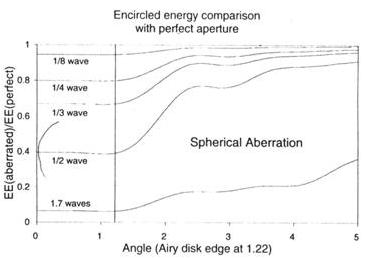
Рис. 10-6. Круговая энергия открытых апертур страдающих от сферической аберрации деленная на круговую энергию совершенной циркулярной апертуры.

Этот эффект выпаривания энергии из сердцевины изображения существует для поддержания более менее равного (но, более тусклого) диска Эри окруженного затуманиванием, уменьшающимся с расстоянием. Детали планет страдают в известной степени, потому, что темные отметины низкого контраста часто очень близки к ярким обласям, которые растекаются или размываются. МПФ схема показывет, что худший эффект погрешности коррекции начинает иметь место для отметин поверхности имеющих разделения около 1/3 - 1/2  предела разрешения инструмента. Поэтому, телескоп имеющий аберрации, способный разрешать звезды разделенные 1 угловой секундой показывает детали планет (такие как полосы разделенные менее чем в пределах 2 или 3 секунд дуги) с заметно пониженным контрастом.

10.5.2. Образцы дифракционных структур звездного теста коррекционной ошибки.

Во время проведения звездного теста, вы можете пожелать рассматривать изображение через цветной фильтр для избежания эввектов перемешивания цветов.  Поскольку максимальная чувствительнсть человеческого глаза приходится на желто-зеленую область, вы вероятно сможете получить наибольшую информацию, используя фильтр основывающийся на этих цветах. При употреблении искуственного источноика (такого как фонарик), некоторая непредвиденная фильтрация причиняется более низкой цветовой температурой нити накаливания.  Вы можете открыть для себя полезные эффекты фильтрации в течение проведения звездного теста телескопа, используя с этой целью Арктур во время дымчатой ночи. Звезда по природе желтая, но так сильно окрашивается прохождением света сквозь дымку, что становтся оранжевой. Немногие цветные фильтры обрезают все света других спектральных полос, однако. Вам не стоит ожидать монохромных картин дифракции вичисляемых здесь для их точного воспроизведения.

Несомненно, вы вольны пытаться применять и другие фильтры, но знайте, что когда вы идете от синего к красному ошибка в длине волны уменьшается. Красные фильтры могут помочь вычесть малоамплитудный мусор из изображения дифракционного образца, когда вы пытаетесь рассматривать широкие деформации волнового фронта.

Поведение пред-фокального изображения  обрисовано на рис. 10-7, где сферическая аберрация изменяется от 0 до 1.7 длин волн. Все коррекционные погрешности отличаются от совершенной апертуры, но первое кольцо блестит сильно, для аберраций больших, чем ¼ волны. Поскольку использование вторичного зеркала так распространено, похожее сравнение проводится для 33%-но экранированной апертуры – показно на рис. 10-8.

За-фокальное поведение представлено на рис. 10-9. и 10-10. с каждой последующей парой имеющей слегка усугубляющееся недоисправление. Каждый из этих образцов вычислен для 10 длин волн аберрации дефокусировки. Тяжелый случай  1.7 длины волны вычислен для переисправленности (заметьте противоположное поведение образцов). Здесь сильное внешнее кольцо появляетя позади (снаружи) фокуса. Мы наблюдаем срезы рожкообразной каустики на этих рисунках. С одной стороны фокуса, рожок срезан вблизи мундштука, потому так много энергии концентрируется вблизи центра. Все же, много еще энергии проливается в окружающую область, делая внешний вид диска затуманенным.

Снова, поведение впереди (внутри) фокуса показано для 33%-ой преграды на рис. 10-11. И 10-12. Погрешность в 1.7 длины волны не точно воспроизводит образцы ожидаемые в Космическом телескопе Хаббла до починки, но это поведение доброе приближение.

С меньшим количеством сферической аберрации, вам необходимо делать меньшую дефокусировку, чтобы показать образцы хорошо. Рис. 10-13. показывает проявление аберрации всего лишь в 5 длин волн.

10.5.3. Оценка серьезности проблемы.

Коррекционные погрешности создают заметный контраст между внутри-фокальными и снаружи-фокальными образцами звездного теста. Опытный наблюдатель при великолепых условиях може уверенно обнаружить ошибку менее 1/10 длины волны и даже 1/20 длины волны (Вельфорд 1960). Иронически говоря, звездный тест на сферическую аберрацию чувствителен почти что через-чур. Он настолько проницателен, что почти любой телескоп невыдержит случайной проверки.

Высокоразрешающая система обнаружения света позволила бы произвести измерения за пределами расширенного звездного диска и определить, как в точности аберрация влияет на телескоп.  Поскольку глаз радиометр ужасный, ему нельзя верить при измерении яркости.  Люди, пользующиеся глазами для определения звездной величины переменных звезд, преуспевают лишь в том случае, если они следуют осторожной методике использования похожих звезд сравнения. Оценивание яркости протяженных объектов (как расфокусированные звездные диски) занятие вообще безнадежное.  Тщательно калиброванные дтачики света применялись для такой работы, но подобное решение требует исключительно точного знания  рассояния дефокусировки. Это непрактично для тех, кто желает провести быстрый звездный тест. (К примеру, об этих измерениях читайте у Burch 1985.)

Должен быть разработан метод, который использует силу зрения вместо его слабости, некоторый инструмент, что не полагается на абсолютную способность глаза определять яркость. Намек на этот метод появляется в Любительском Телескопе Вильяма Ф.А. Эллисона, который был перепечатан в Построении Любительского Телескопа Книга Первая: (Инголлс 1976)

Вполне легко видеть, посредством за-фокальных изображений звезды, каково состояние коррекции зеркала. Истинно откорректированное зеркало, позади фокуса, даст расширенный диск, однородно освещенный, за исключением неясных тусклых следов дифракционных колец, имеющий чистый, четко определяемый край и круглое черное пятно в центре. Это черное пятно - тень от плоского зерала (the flat), и должно оставаться одного и того же размера на равных расстояниях перед и за фокусом.

Если оно шире внутри фокуса, зеркало недоисправлено, если оно шире снаружи, переисправлено. И много раз за ночь при различной температуре, писатель наблюдал, зеркало проходящее через все эти фазы в течении не очень долгих минут, изменения черного пятна верно соответствовавшие изменениям термометра…[курсив по оригиналу]

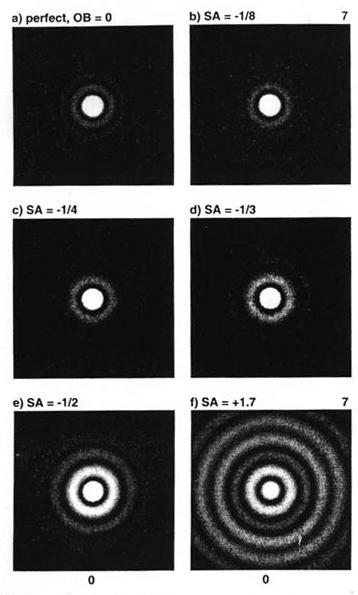
Рис. 10-7. Сфокусированные образцы для 0, 1/8, ¼, 1/3, ½, и 1.7 длин волн аберрации низкого порядка. Апертура не экранирована.

Рис. 10-8. Предфокальные образцы для a) 0, b) 1/8, c) ¼, d) 1/3, e) ½, и f) 1.7 длин волн сферической аберрации низкого порядка. Апертура имеет 33%-ую центральную круговую преграду.

Рис. 10-9. Недоисправленные апертуры внутри фокуса (слева) и снаружи (справа).Аберрация дефокусировки ±10 длин волн. a) 0, b) 1/8, c) ¼ длин волн сферической аберрации низкого порядка. Апертура открыта.

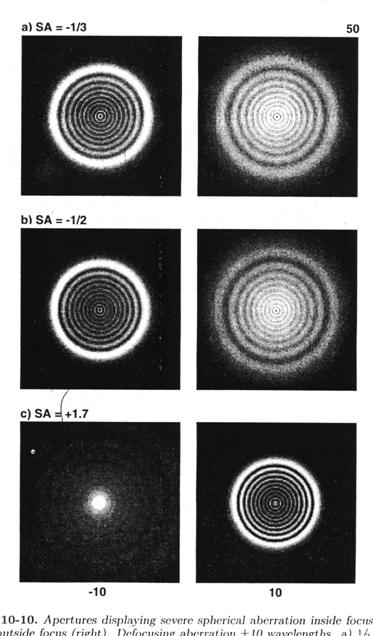
Рис. 10-10. Апертуры показывающие серьезную сферическую аберрацию перед фокусом (слева) и за (справа). Аберрация дефокусировки ±10 длин волн. a) 1/3 длины волн недоисправленное, b) ½ длины волны недоисправленное, c) 1.7 длины волны переисправленное. Апертура открыта.

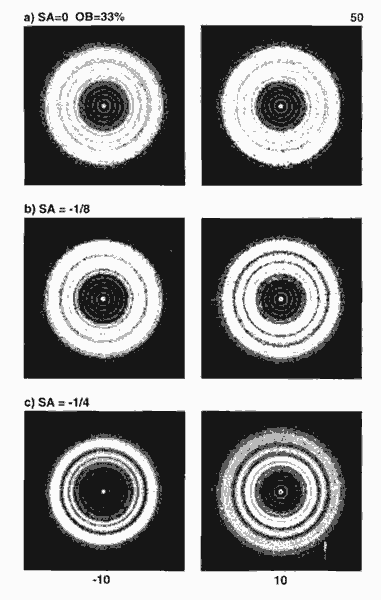
Рис. 10-11. Недоисправленные апретуры внутри (слева) и снаружи (справа). Аберрация дефокусировки ±10 длин волн. a) 0, b) 1/8, c) ¼ длин волн сферической аберрации низкого порядка. Апертура на 33%  экранирована.

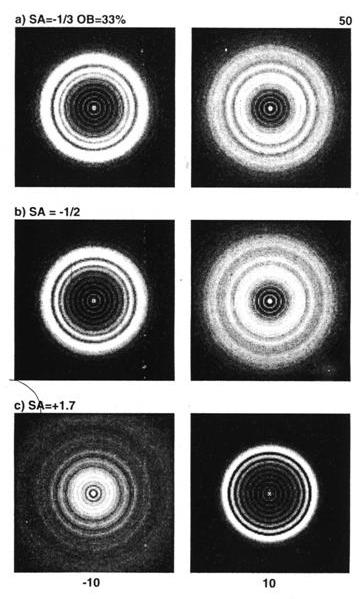
Рис. 10-12. Серьезная сферическая аберрация внутри (слева) и снаружи (справа). Аберрация дефокусировки ±10 длин волн. a) 1/3 длины волн недоисправленное, b) ½ длины волны недоисправленное, c) 1.7 длины волны переисправленное. Апертура на 33% экранирована.

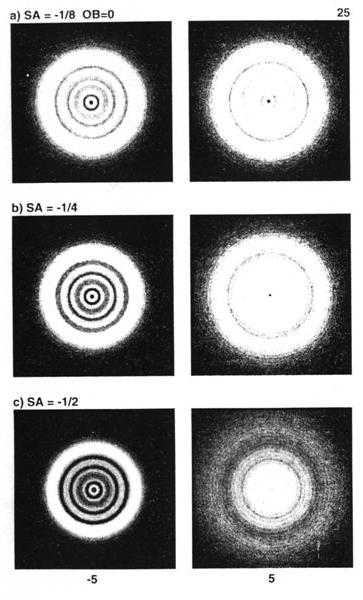
Рис. 10-13. Недоисправленные апретуры внутри (слева) и снаружи (справа). Аберрация дефокусировки ±5 длин волн. a) 1/8, b) 1/4, c) 1/2 длин волн недоисправлено. Апертура отркрыта.

Как оказалось, эти комментарии были вставлены в дискуссию представляющуюся критичной для звездного тестирования. Возможно многие Эллисоновские читатели были сбиты с толку этой дискуссией и пришли к мысли, что звездный тест неадекватен. Эллисоновы доводы были, однако, справедливыми. Зеркальные стекла распространненые в то время были непригодыми для тестирования в окружающей среде с быстро меняющейся температурой. Любой тест дал бы отрицательные результаты в такой ситуации.

Современные материалы, лежащие в основаниях зеркал в серьезно меньшей степени склонны деформироваться под воздействием температуры. До тех пор пока телескоп имеет атмосферную температуру, оптика ведт себя довольно приемлемо. Тест надежен при медленно меняющихся внешних температурах.

В любом случае, пятно тени предоставляет тестировщикам возможность оценить аберрацию. Рис. 10-14а демонстрирует продольный срез через точку фокуса совершенной апертуры. Объектив или зеркало слева, направление наружного фокуса справа (для объяснения пометок см. прил. D). За исключением активности пятна вдоль оси, выглядящей как бусины на нитке, зафокальный профиль гладок и неинтересен. На рис 10-14b мы рассматриваем ту же самую ситуацию с 33% процентой центральной преградой. Апертура, напротив, – совершенная и ситуация симметрична.

В темных конусах появляющихся из центра, тень диагонали, кажется, выпадает из дефокусированного изображения на ограниченном расстоянии рядом с фокусом. Поскольку изображение довольно мало, яркое пятнов центре откладывает появление центрального препятствия, пока аберрация дефокусировки не достигнет двух длин волн с каждой стороны фокуса. (см. гл. 5 для перевода дефокусирующей аберрации в движение фокусера). Окуляр должен перемещаться немного дальше, пока пятно не определится четко. Тем не менее, заметтье, что точки разрыва для совершенного зеркала сбалансированы; они располагаются на одинаковом расстоянии с обеих сторон фокуса.

Что происходит, когда мы добавляем некоторое недоисправление в экранированную апретуру? Ответ на рис. 10-15.

Первый предмет интереса, что точка наилучшего фокуса смещается немного вперед с прогрессивно усугубляющимся проявлением недоисправления.  Аберрация была введена с помощью многочлена Цернике, но у этих функций небольшой сдвиг фокуса для экранированных апертур.

Следующая особенность - малый размер диска внутреннего фокуса по сравнению с внешним фокусом, но это заметно на рис. 10-12. приведенном ранее, который был подправлен за этот сдвиг. Не сужествует некоторой уникальной точки для искаженного фронта волны.  Приближаясь к фокусу, волновой фронт должен сойтись и изменить форму, проявляя себя в этих разных размерах.

Консервация энергии всегда съиграет свою роль. На рис. продольного среза, не может быть проведена ни одна вертикальная линия, чтобы не упереться в освещенную область. Интенсивность не позволяет себе отключаться повсеместно в плоскости среза.

Рис. 10-14 Продольный срез через фокус a) круговой неэкранированной апертуры b) 33%-но экранированной апертуры. Ни один из оразцов не содержит ни одной связанной с ним аберрции. Срез взят в пределах аберрации дефокусировки от –8 длин волны до +8. Угол окантовки в 32l¦/D соответствует прослеживающему лучи краю геометрической тени ±8 длин волн дефокусировки. Так, картина сжималась, пока не стала напоминать конус системы ¦/1.

Фактически, если мы очень осторожно проследим полную энергию вдоль всех значений дефокусировки, мы обнаружим, что она равна тому же количеству прошедшему сквозь апертуру. Затяжки и узелки всего лишь упорядоченность. Появление яркого кольца контрбалансируется темным кольцом появляющимся где-нибудь в другом месте на плоскости среза.

Темные конусы тени вторичного зеркала больше не находятся на равных смещениях в присутствии коррекционной погрешности. Это выглядит понятнее на схемах рисунка 10-16. На диаграмме ¼ длины волны, центральное препятствие не обнаруживается, до удвоенного расстояния (½ длины волны) от наилучшего фокуса.

Два эффекта сговорились сместить точку разрыва тени вторичного зеркала. Один - группирование энергии вокруг края рожкообразной каустики с одной стороны фокуса.

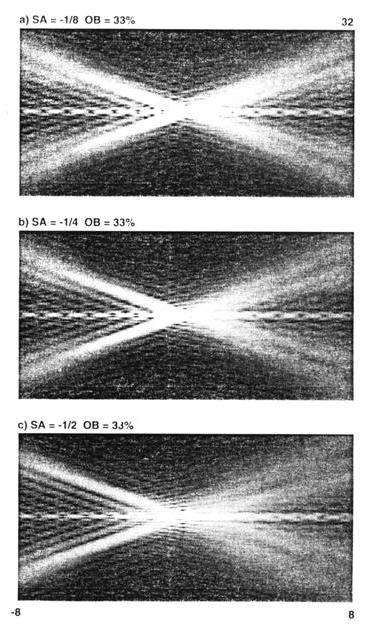
Рис. 10-15. 33%-экранированные апертуры показывают различие расстояний появления тени вторичного зеркала от центра дифракционного диска. Коррекционная погрешность а) –1/8 длины волны, b) –1/4 длины волны и с) –1/2 длины волны (все недоисправлены).

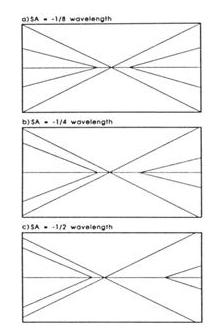
Рис. 10-16. Диаграмы представляющие эскизы общего поведения рис. 10-15. Расстояние возобновления появления тени вторичного зеркала заметно отлично, если коррекционная ошибка превышает ¼ длины волны.

Эта жестокая экскавация энергии из центра позволяет тени вторичного зеркала вырываться вперед более быстро (раньше). Другой эффект скучивание энергии к мундштуку рожка с другой стороны фокуса. Эта интенсивность заполняет тень вторичного зеркала и задерживает ее возобновленное появление. Тень втричного зеркала не выдается до тех пор пока окуляр не будет выдвинут достаточно далеко за каустическую область.

Для сферической аберрации низкого порядка может быть определен некоторый критерий. Мы будем требовать чтобы отношение расттояний разрыва было бы не более чем 2:1. Конечно, оценка должна производиться на 33%-о экранирванной апертуре.  Этот тест отличен от описанного Эллисоном. Он дефокусировал на равные расстояния и сравнивал размер теней. Здесь мы будем оценивать относительные расстояния с каждой стороны фокуса, на которых тень четко проявляет себя.

Такой критерий был бы черезвычайно слаб, если бы мы основывались лишь на одной теоритической мысли.  Он происходит от продолжительного опыта звездного тестирования телескопов для которых проводились и другие тесты. Этот допуск ни в коем случае не абсолютен. Возобновление появления тени зависит от яркости звезды, видимости, и смеси с другими аберрациями. Человек проводящий тест должен принимать в расчет основное рабочее поведение телескопа до того как отвергнуть его из-за отрицательного результата теста «2:1». Тем не менее я еще не видал зеркала имеющего коррекционную погрешность в ¼ длины волны (как определяется по зональному тесту Фуко)  дававшего низшее отношение.

10.6. Тест на коррекцию.

Этот тест отношения 2:1 полезен и для других телескопов помимо рефракторов. Телескоп следует экранировать даже если в его конструкции и не присутствует вторичного зеркала. Рефракторы можно было бы   экранировать размещая в центре кусочки бумаги над входным отверстием телескопа.

Снятие показаний смещения вовсе не хорошо управляемый процесс. Если преграда составляет 25% отрезок сдвигается плоть до 3:1. Поскольку большинство Ньютонов имеют препятствия меньшие чем 33%, этот тест может быть стандартизован посредством создания увеличенных масок прикрепляемых с обрантой стороны крестовины. Конечно, естественная преграда большинства Шмидт-Кассегренов уже очень тесно приближается к 33%.

Также, обнаружение точки разрыва тени препятствия намного более простой процесс на телескопах среднего и высокого фокального отношения. Много проще снимать результаты на телескопах с фокальным отношением более f/8. Трудность сделать оценку на короткофокусных инструментах ужесточается стойкой и шестернями фокусеров, а также крошечной глубиной фокуса.

Эта процедура повидимому хорошо работает в белом свете, поскольку он имея множество цветов склонен замывать минимумы в окружающих дифракционных кольцах, или по крайней мере делает их менее различимыми. Вторичное проявляется во всех цветах, но детали в диске зависят от конкретного цвета. Если только вы не тестируете рефрактор, постарайтесь убрать фильтр для проверки размера пятна.

Источник не должен быть слишком ярким. Если вы исследуете изображение вблизи фокуса, рассматривание яркой звезды  могло бы подавить глаз и сделать видимость деталей в центре изображения затруднительной. Если вы проводите тест на искусственном источнике, вам может потребоваться переместить излучатель на большее расстояние, использовать меньший отражатель, или окулярный фильтр нейтральной плотности. Если телескоп кажется имеет необычно большое смещение, повторите тест снова на звезде послабее.

Поведение одного из цветов представлено на рис. 10-17. Диаграммы следуют от слегка внутри фокуса слева вверху до немногим дальше снаружи фокуса справа внизу. Учитывайте, что эта диаграмма представляется здесь со слишком большим увеличением.Если у вас возникли трудности с видимостью где тень непрерывна и силно появляется снова на рис. 10-17, расположите рисунок на некоторой дистанции. Вы обнаружите, что тень не очевидна на самом деле до тех пор, если не углубиться хорошо за фокус. Тень выглядит имеющей равное центральное подавление на –1.5 и 3.75 аберрациях дефокусировки.

3.75 по сравнению с 1.5 кажется немного больше оценки 2:1, но вспомните, что эта переходная точка груба. Множество было сделано компромиссов при создании этих образцов изображения на бумаге. Наиболее важное приближение  в том что рисунки не самосветящиеся. Абсолютная яркость и контраст изображения также были сдвинуты с тем чтобы они могли быть отпечатаны на средстве с ограниченным динамическим диапазоном. Точка на которой вам следует побеспокоиться о коррекции вашего телескопа когда отношение просттирается до 3:1.

Дополнительный эффект дефокусированной сферической аберрации показан на рис. 10-17. Когда вы дефокусируете по направлению к раструбу каустики (внутри фокуса для недоисправленной оптики), тень очерчивается резко и чисто. С другой стороны, тень сперва появляется, как небольшое центральное потемнение или пупуок. Появившись тень вторичного зеркала разворачивается или распускается. Точка несомненного появления менее четка но все еще ощутимо отлична чем с другой стороны. Из-за этой неуверенности, метод не считается точным измерением. Это единственный способ обнаружить необыкновенные количества коррекционной погрешности которые могут калечить ваш телескоп. Вы не можете использовать этот метод отношения для точного измерения сферической аберрации.

Если с другой стороны хороший телескоп не проходит этот тест, вы просто можете иметь вмешивающуюся аберрацию инго типа. Если вы подозреваете, что положение разрывае тени дает вам неверный ответ, перейдите к сравнению образца фиксированного расстояния (как на рис. 10-13.) высматривая величину дефокусировки из таблю 5-1. Помните о предупреждении Эллисона. Позольте оптиске совершенно остыть. Пирекс лучший материал, чем стекло, но его форма не совсем не зависит от изменения температуры.

10.7. Сферическая аберрация более высокого порядка.

Иногда коэффициент A¢₆ выбрасывается или не поправляется. В большинстве телескопов эта аберрация не имеет большого значения, но она может представлять проблему для необычных инструментов.

Например, форма пластины корректора Шмидта сходна с кривой четвертого порядка в ур. 10.3 с отличной величиной r² разумно выбранной для уменьшения потенциальной хроматической аберрации. Короткофокусное сферическое главное зеркало производит аберрационную функцию с множеством членов в расширении в ур. 10.2, но коррекционная пластина способна к простому исправлению этих членов только до четвертого порядка. Небольшая величина аберрации шестого порядка может остаться нескорректированной. Разнообразные виды объективов могут также добалять пустячные количества сферической аберрации «вторичного зеркала» шестого порядка на волновом фронте (Кингслэйк 1978, стр. 114).

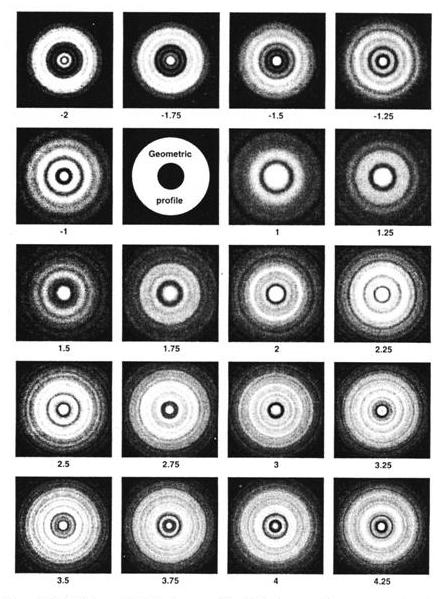
Рис. 10-17. Дефокуисрованные звездные изображения 33%-о экранированной апретуры имеющей ¼ длины волны недоисправленность. Каждая рамка увеличена так что совершенный геометрический профиль имеет тот же размер что помеченная рамка.  Таким образом, край находится в 10 угловых единицах для дефокусировки в 2 длины волны и в 20 для 4-х, и т.д. Снизу каждого квадрата стоит метка  аберрации дефокусировки в длинах волны.

Сферическая аберрация более высокого порядка спокойно может не учитываться в большинстве инструментов.

10.7.1. Образцы дифракционных структур звездного теста сферической аберрации более высокого порядка.

Коэффициент A¢₆  в ур. 10.3 приносит образцы рисунка 10-18. Подобно коррекционной погрешности четвертого порядка, с противоположным знаком, A¢₆ дает результатом эти образцы перевернутые в фокусном направлении.

Погрешность выглядит хуже в звездном тесте, чем ведет себя на картинке.  Чтобы уменьшить отношение Стреля до той самой 0.8 величины которую оно имеет для ¼ длины волны сферической аберрации более низкого порядка, A¢₆  должно было бы возрасти до 0.4 длины волны.

Описание каустики более высокого порядка как рожка наполовину втянутого взад сквозь самого себя помогает объяснить эти сложные структуры. Образцы звездного теста коррекционной погрешности, что появлялись ранее в этой главе, уходили от яркого внешнго кольца с одной стороны фокуса к диффузной яркой сердцевине с другой стороны. Здесь диффузная яркая сердцевина проявляется с той же стороны фокуса как дыра в центре (рис. 10-18, -3 длины волны дефокусировки).

По этой причине, сферическая аберрация более высокого порядка может быть названа «колцевой аберрацией». Она несет более чем случайное сходство с зональными дефектами, описываемыми в главе 11. В самом деле, эта аберрация может рассматриваться, как передача зональных аберраций.

Конечно, сферическая аберрация более высокого порядка редко видна в чисто опозноваемой форме. Как остаточная (вычитная) аберрация в нормальном телескопе, ее амплитуда очень низка. Эта аберрация обычно затопляется другими эффектами. Я видел ее небольшое количество только в Шмидт-Кассегрене, где глубокая тень вторичного была спарена с ослабляющейся яркостью к краю внефокального дифракционного диска. Другая сторона фокуса обнаруживала противоположное поведение, со светлой тенью вторичного зеркала и сильным внешним кольцом показывающимся одновременно. Единственная причина по которой я был спосбен недвусмысленно видеть  эту маленькую аберрацию было почти полным отсутствием простой коррекционной погрешности в исключительно хорошем инструменте.

10.7.2. Фильтрация сферической аберрации более высокого порядка.

График фильтра сферической аберрации более высокого порядка  представлен на рис. 10-19. Ясно, ¼ длины волны аберрации не влияет на оптику столь серьезно. Повреждение не становится значительным пока аберрация не возрасла до 0.4 длин волны. Худшая часть уменьшения присутствует на более низкой пространственной частоте, чем это представлено на рис. 10-5. для сферической аберрации более низкого порядка.

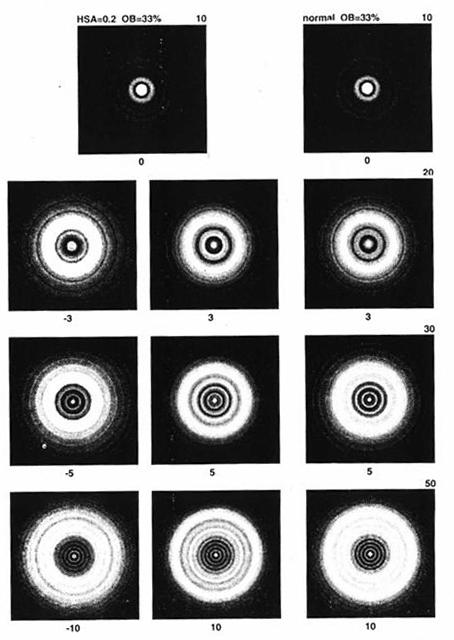
Рис. 10-18. Образцы звездного теста для 1/5 длины волны сферической аберрации более высокого порядка в наилучшем фокусе. Препятсятвие 33%.

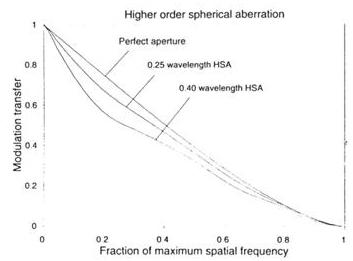
Рис. 10-19. Кривые МПФ вызванные 0.25 и 0.4 длины волны сферической аберрации более высокого порядка.

В этом случае падение присутствует у приблизительно 20% от максимальной пространственной частоты вместо 35%. Если вспомнить, что максимальное разрешение 200-мм апретуры около 0.6 циклов на секунду дуги, эта аберрированная система передает детали поверхности разделенные менее, чем 3-я угловыми секундами с пониженным контрастом.

Когда «локоть» кривой МПФ проявляется дальше слева это знак более волнистого вида функции аберрации. Погрешность поверхности становится более ограниченной. Когда оптическая погрешность становится меньше и проходит сквозь более частые решетки, соответствующая МПФ демонстрирует более крутое падение на низких пространственных частотах. Когда оптические погрешности становятся более ограниченными,  МПФ-ы на высоких пространственных частотах также уменьшаются, но не осциллируют сильно. Повреждение уже почни нанесено на низких пространственных частотах. Однако, должно быть подчеркнуто, что чистая сферическая аберрация более высокого порядка этой величины вероятно не может вызвать неприятностей у обычных телескопов. Если оптика сфабрикована плохо, большая часть аберрации выражается в простой коррекционной погрешности четвертого порядка.

10.8. Компактный, Унифицированный стандарт для качества оптики.

Наблюдатели и изготовители потребительских телескопов сходно склонны раздерять аберрацию и препятствие в различные разделы, обращаясь с этими двумя как с несравнимыми феноменами. Однако, может быть определен единый стандарт объединяющий их обоих. Он основывается на отношении круговой энергии (EER ( q ) ), или какая часть энергии от точечного источника фокусируется в крошечном центре определенного углового радиуса в фокальной плоскости. Это число сравнимо с той же частью для совершенной неэкранированной апретуры равного диаметра. Мы уже видели как отношение круговой энергии ведет себя в случае чистой преграды (рис. 9-1.) и простой сферической аберрации низкого порядка (рис. 10-6. выше), но можно было бы определить такое отношение для смеси обоих.

Отношения круговой энергии  представленные на рис. 10-6 совершенные кривые. Для одного числа, что представляет критерий качества, необходимо взять EER ( q ) величину определенного значения  q . Всает вопрос: какой угол наилучший?

К несчастью ни один из углов не будет последним словом в определении качества. Мы могли бы выбрать некоторый угол (или круг) весьма близкий к центру изображения, или EER ( q ® 0 ).  Это число близко к перпендикулярному отношению яркости у центра дифракционного диска. Фактически, оно идентично отношению Стреля в неэкранированных апретурах. EER взятое близь центра изображения, однако, кажется черезмерно толерантно к преграде, как демонстрирует рис. 9-1. EER ( q ® 0 ) не опускается ниже 0.8 – отсекающей точки хорошего качества оптики в отношении Стреля -  пока препятствие не превышает 45%. Можно было бы определить так же фактор качества как EER внутри круга радиуса q  = 1.22l/D (ур. 1.1), или край дифракционного пятна Эри. Рис. 9-1 показывает, что величины EER (1.22) значительно прогибаются, и начали даже подниматься снова.

Несколько произвольно, эта книга будет использовать угловой радиус q  = l/D, или угловой промежуток, где МПФ всегда сводится к нулю. Этот угол имеет практическое преимущество над схватыванием подходяще экранированных апертур в их нижних точках на рис. 9-1. и имеет философское преимущество над постоянным отношением к максимальной пространственной частоте графика МПФ. Это отношение будет называться  EER(1). На рис. D-2, вы можете видеть, что край рамки находится у угла 1.22l/D. Так круг нарисованный здесь, сидел бы в темноте посреди двух колец. Интегрированная область EER(1) слегка внутри яркого края диска.

EER(1) апертур смешивающих две оптические проблемы: экранирования и сферической аберрации более низкого порядка (Цернике) собраны вместе в табл. 10-1. В неэкранированном верхнем ряду мы видим поведение очень похожее на отношение Стреля. Четверть длины волны сферической аберрации все еще выдает ухудшение EER(1) до 0.8. Это вторая ось, которая, однако, наиболее интересна. Можно сравнить потерю отношения круговой энергии экранированной апертуры, но иначе (?) совершенные апертуры. EER(1)=0.8 для преград слегка меньших 33% полного диаметра.

Заметьте, что преграда не всегда уменьшает качество. Случай коррекционной ошибки в ½ длины волны демонстрирует любопытную инверсию, с увеличением преграды служащей для скрытия плохой фигуризации.

Таблица 10-1

EER(1) для апертур со сферической аберрацией более низкого порядка.

Волновой фронт рефокусирован.

Преграда – закрытая часть диаметра.

Коррекционная погрешность пика-к-подошве в неэкранированной апертуре.

Мой личный опыт с большим количеством телескопов имеющих разную величину коррекционной погрешности наводит на мысль о следующих эмпирических цифровых данных. Эти отсечки неизбежно туманны, и «хорошая» точка умышленно выбрана для соответствия отношению Стреля (т.е. 0.8), оптика условно называется «дифракционно-ограниченной».

1.       0.88 - 1.00 великолепный до совершенного

2.       0.80 - 0.88 хороший до великолепного

3.       0.70 - 0.80 слабый до хорошего

Единственно приемлемые инструменты с EER(1) ниже 0.70 телескопы специального назначения, такие как астрокамеры и широкоугольные телескопы. Ни один инструмент, имеющий 1/3 длинны волны коррекционной погрешности,  даже если неэкранированный, не достигает этого минимального стандарта. Ниодна апертура с преградой превышающей чуть более 40%, даже если сфигурирована совершенно, никогда не достигнет его.

10.9. Допустимые погрешности.

Все телескопы делаются с некоторой сферической аберрацией. Совершенный Ньютоновский параболоид, к примеру, недостижимая цель в промежутке бесконечного числа вытянутых сфероидов и гиперболоидов. Вопрос в том насколько телескоп страдает от этого бремени. Когда EER(1) превышает 0.88 или около того, сферическая аберрация удовлетворительно мала и оптика справедливо могла бы называться «совершенной».

Мы видели в гл. 3 как модуляционные передаточные функции индивидуально выстраивались. Большиноство экранированных телескопов уже качаются на краю. Не надо многого чтобы их столкнуть. По такой логике, нам следовало бы быть нетерпимыми к любой коррекционной ошибке, но это отношение нереально.

Коммерческая телескопическая оптика всегда корректировалась с допуском около ¼ длины волны. Способ, которым устанавливается точность, изменился, но строители коммерческих телескопов все еще фабрикуют туже самую ¼ длинны волны оптику, как всегда.

Поймем некоторый факт. Доведение объективов до высшей точности, чем ¼ длины волны, дорого. Соотношение цена – качество, похоже на соотношение цена – диаметр. Прибыльные улучшения в точности поверхности стоят намного дороже потому, что мы платим не за стекло, а драгоценное время оптика. Ради лучшего или худшего (как правило, худшего), покупатели рассматривают цену как сильный решающий фактор.

Действительно ли точность так необходима?  В неформальных испытаниях, телескоп с четвертьдлинноволновой коррекционной погрешностью оказалось затруднительно отличить от  оченьхорошего телескопа если только видимость не совершенна и наблюдатель не опытный ( Ceravolo и др. 1992; также см. гл. 15). Для большинства людей наблюдающих в средних условиях ¼ длинны воны коррекционной погрешности представляет собой приемлемый компромисс между ценой и качеством оптики.

В предидущем разделе мы определили апертуры с отношением круговой энергии большем 0.88 как великолепные. Мы видим, что это обозначение применимо только к левому верхнему углу табл. 10-1 т.е., к преградам меньшим 25% или коррекционной погрешности менее 1/5 длины волны. Заметим, что 25%-о экранированная апертура лишь с 1/6 длины волны коррекционной погрешности все еще «хороша» с 0.81, но, что 15%-о экранированная апертура с ¼ длины волны погрешности ниже обреза с 0.78. Урок понятен. Тщательная фигуризация позволяет телескопу  отделаться от других сложностей.

Лично, я нахожу изображения оптики, подталкиваемые к пределу Рэлея, слегка слишком мягкими. Однако, из телескопов, что я тестировал, большинсво очевидно работавших нехорошо, были много хуже ограничения Рэлея. Четверть длины волны коррекционной погрешности почти приемлема если это единственная заметная проблема. С разумной 25% преградой такая апертура имеет EER(1)=0.74 и передаточную функцию лучшую, чем совершенная, неэкранированная апертура в половину или 2/3 ее размера. Даже с оптическими проблемами этой величины, типичный 6-дюймовый f/8 рефлектор поменьшей мере настолько хорош насколько великолепный 3 – 4 дюймовый апохроматический рефрактор. А на некоторых пространственных частотах и лучше.