Приложение С.

Ральф Дакин опубликовал точные выражения для малой оси и смещения в Sky & Telescope несколько лет назад, но эти выражения даны для больше для удобства вычисления, чем для показа. Отсюда, уравнения слегка загадочны и повод для ошибок, когда публикуются во вторичных источниках. Эта ситуация не облегчалась досадной типографической ошибкой в оригинальной статье. Ошибка была исправлена несколькими месяцами позже, но исправление часто пропускалось и неправильные выражения прогрессировали дальше в любительской литературе (Дакин 1962, erratum 1963).

Эти величины нетрудно получить, и кое что можно узнать из рассматривания логики аналитической геометрии, так что они здесь получены заново. Последующие формулы внешне отличаются от выражений Дакина, но они дают те же ответы. Различия вероятно вызваны положениями систем координат. Такие изменения зачастую ведут к якобы другим формулам.

С.1 Вычисление

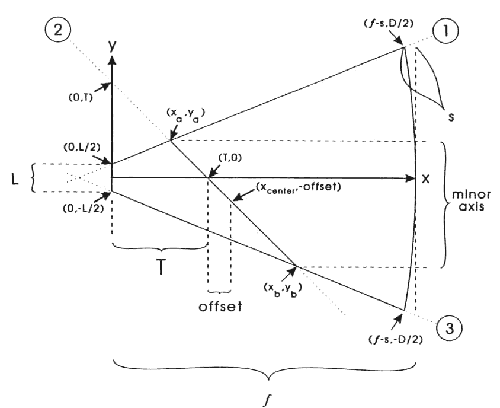
Рис. С-1 показывает развернутый Ньютон и определяет различные величины полезные в этом вычислении. Эти переменные: ¦ - фокусное расстояние; D – диаметр зеркала; s – сагитта или глубина этого зеркала; T – расстояние от фокальной плоскости до центра трубы; и L – диаметр полностью освещаемой области в фокальной плоскости. В этом вычислении, я определю значения малой (короткой) оси диагонали и боковое или нижнее смещение ее центра. Координатная система определяется ее происхождением в центре фокальной плоскости. х-ось проходит через центр зеркала, и у-ось в стороне от оптической оси.

Существенны три линии рисунка С-1. Линии №№1 и 3 следуют от краев полностью освещенного поля до краев зеркала. Линия №2 направлена вдоль поверхности диагонали. Мы знаем что она под 45° и поэтому касается двух осей в указанных точках имея координаты (Т,0) и (0,Т). Сходно, мы знаем координаты двух точек вдоль каждой из линий №№1 и 3, и мы можем использовать это знание, чтобы получить определяющее уравнение этих линий также.

Раз уравнения линий известны, точки пересечения на дальних краях диагонали могут быть вычислены. Эти пересечения имеют координаты (x_a,y_a) и (x_b,y_b). Эти точки все что требуется, чтобы получит и малую ось и смещение. Малая ось:

(С.1)

(С.2)

Линии имеют общую форму y=mx+b, где b - у-пересечение и m - склон. Линию №2 определить легче всего, и осмотрев можно присвоить ей уравнение

(С.3)

(С.4)

(С.5)

Мы можем переименовать величину (D-L)/2(f-s)º n. Все три уравнения могут быть суммированы как

(С.6)

Постановив y₁-y₂, мы можем определить координату х_а как

(С.7)

(С.8)

(С.9)

(С.10)

(С.11)

Последние выражения С.10 и с.11 исчерпывающи. Они требуют лишь выражения для сагитты. Парабола фокуса f определяется уравнением x=f-(y2/4f), и точная сагитта получается оценкой сдвига по х на оси и у-значения края, D/2:

(С.12)

легко посчитать (по ур. С.10), что МА=1.43423950 дюйма. Это число хорошо сравнимо с результатом 1.43423955 с применением формулы Дакина перепечатанной у Тексеро. Смещение=0.056646217 дюймов там, и 0.056646220 здесь. Легкая разница вызвана ошибкой в следствие отбрасывания членов. (Вычисления у Тексеро исполнялись до больших знаков десятичной дроби для сравнения.)

С.3 Аппроксимации

Приблизительно точные значения не так трудно вычислить с распространенными возможностями калькуляторов и компьютеров. Программы электронных таблиц особенно удобны для вычислений таких как эти, но кое-кто может пожелать более компактной формы аппроксимации.

Заметьте, что у ур.С.10 и С.11, коэффициент1,(1-n²) может быть аппроксимирован как 1+n². У большинства зеркал, величина (D-L)/2(f-s)º n очень близка к (D-L)/2f. Заглавная F фокусное отношение, поэтому

(С.13)

где наименьшие члены не принимались в расчет.

То же разложение может быть сделано с уравнением для МА, снова игнорируя исключительно крошечные члены, чтобы получить ответ

(С.14)

Проверочный случай выше был пересчитан по ур. С.13 и С.14 и ответы МА=1.424 и Смещение=0.057 дюйма, очень близки к точным цифрам. Конечно, у очень маленькой, полностью освещенной области фокальной плоскости, эти величины приближаются к MA=T/F и Смещение=T/4F².

 

Реклама: мебель в коттедж: антикварная мебель продажа